03_Parte3

Questo file è la rielaborazione delle slide 03_Parte3.pdf

Calcolo combinatorio

Una delle cose più importanti che un informatico deve imparare a fare è contare o calcolare nel modo giusto, in particolare vogliamo essere in grado di contare il numero di oggetti o casi che ci interessano, senza doverli esplicitare uno per uno. Di seguito delle domande di esempio alla quale risponderemo dopo aver introdotto il calcolo combinatorio:

• Domanda 1: Se sto scrivendo un programma che simula il poker, il mio programma deve fare in modo che la probabilità di un poker d’assi servito sia quella giusta. Ma qual è tale probabilità?
• Domanda 2: Quanti sono i codici PIN di una carta bancomat a 5 cifre e quante sono le probabilità che un ladro riesca ad indovinare entro 3 tentativi? Risposta 2 Continuo
• Domanda 3: Quante sono le possibili password fatte di 8 simboli alfa-numerici (maiuscole e minuscole sono diverse) e quanto tempo ci mette un programma che genera 1000 password al secondo a trovare quella giusta? Risposta 3
• Domanda 4: Se dovessi scommettere che in un’aula con 20 persone, ce ne siano almeno 2 che fanno il compleanno lo stesso giorno, scommetterei di si oppure no? E se ce ne sono 30, 40, 50 o più di persone? Risposta 4
• Domanda 5: Quante squadre di calcio diverse posso formare da un gruppo di 50 studenti?

---

Regola della somma

Questa regola ci dice che se vogliamo contare il numero di elementi dell’unione tra due insiemi ci basta sommare la cardinalità dei due insiemi.

• Se denotiamo con $A$ tutte le lettere dell’alfabeto minuscole e con $B$ tutte le lettere dell’alfabeto maiuscole allora il numero di elementi di $A\cup B$ sarà uguale a $|A|+|B|$ e quindi $26+26=52$

---

Regola del prodotto

Questa regola ci dice che se vogliamo contare quanti sono le possibili coppie di elementi, il primo scelto da $A$ e il secondo da $B$ ci basta fare $|A|\ast |B|$.

• Se denotiamo con $A$ tutte le lettere dell’alfabeto minuscole e con $B$ tutte le lettere dell’alfabeto maiuscole allora il numero di coppie possibili sono $26\ast 26=676$
  Più in generale se dobbiamo fare $k$ operazioni di scelta, tali che la prima si può fare in $n_1$ modi, la seconda in $n_2$ modi indipendenti dalla scelta precedenti, la i-esima in $n_i$ modi e quindi la k-esima in $n_k$ modi diversi allora il numero di scelte totali è
• $n_1\ast n_2\ast \cdots \ast n_k$

Avendo le definizioni di queste 2 regole possiamo rispondere parzialmente alle domande 2,3:

• Risposta 2: i codici PIN di una carta bancomat a 5 cifre sono: ^fec4ef
  • $10\ast 10\ast 10\ast 10\ast 10=10^5=100000$
• Risposta 3: Le lettere dell’alfabeto sono $26$ i numeri sono $10$ quindi le cifre alfanumeriche prese in esame sono: ^a39c5a
  • $|A|+|B|=26+10=36$
  • le password fatte da 8 simboli alfanumerici quindi sono sono:
    • $36\ast 36\ast 36\ast 36\ast 36\ast 36\ast 36\ast 36=36^8=\mathrm{2.821.109.907.456}$
  • Un computer che genera 1000 password al secondo ci metterà circa 2,8 miliardi di secondi a generarle tutte

---

Disposizioni e combinazioni

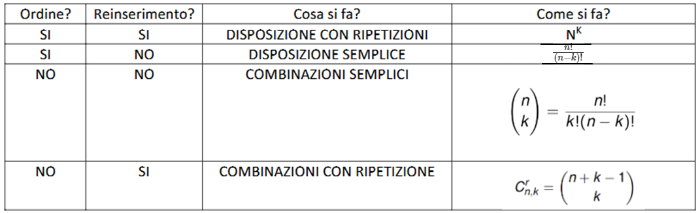La spiegazione teorica dell’immagine che vedi sotto la parte teorica qui è abbastanza inutile.

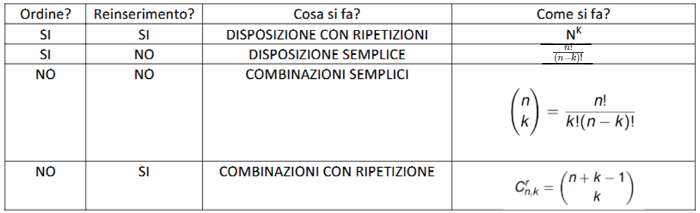
• Se nell’esercizio che sto facendo l’ordine degli elementi è importante guardo le colonne dove “Ordine?” è SI.
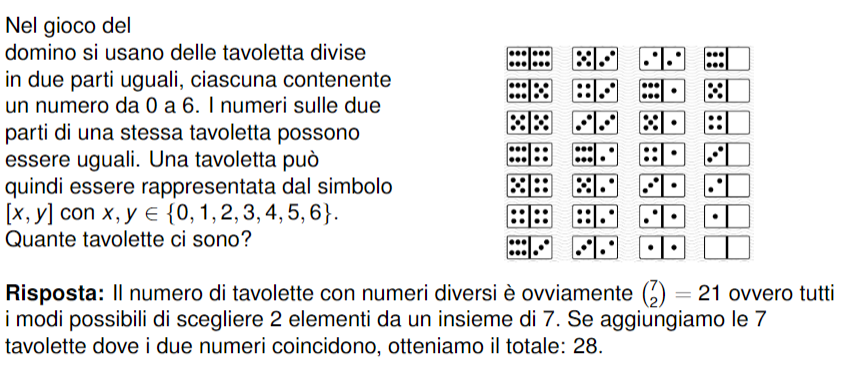
• Se nell’esercizio che sto facendo gli elementi possono essere reinseriti guardo le colonne dove “Reinserimento” è NO. Esercizio 1: Domino Esercizio 2: gruppi di persone Esercizio 3: parola di 4 lettere Esercizio 4: Gelato per tutti

---

Teorema binomiale

Il teorema binomiale è una formula che consente di elevare a qualsiasi numero un binomio così: 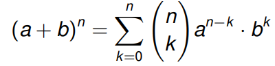Ovvero la sommatoria da $k=0$ fino a $n$ (l’esponente del binomio) della moltiplicazione tra $a^{n-k}\ast b^k$

---

Pigeonhole principle

Nella sua forma più semplice, il Principio afferma che se dobbiamo fare entrare $n+1$ piccioni in una piccionaia che contiene $n$ cassette, allora almeno una cassetta dovrà contenere più di un piccione. Più in generale, se abbiamo $n=km+1$ oggetti da sistemare in m contenitori, allora almeno un contenitore dovrà contenere $k+1$ oggetti.

• se in un cassetto abbiamo solamente calzini bianchi e neri, se peschiamo casualmente 3 volte un calzino, potremo sicuramente formare una coppia abbinata.

---

Probabilità discrete

Introduzione e formalizzazione matematica

Lo studio della probabilità nasce tra la fine del 16esimo e gli inizi del 17esimo secolo, da problemi legati al gioco d’azzardo.

• Le probabilità sono definite su uno spazio di campioni $S$.
• Gli elementi di $S$ sono detti eventi elementari.
• Ogni evento elementare è un sottoinsieme dello spazio dei campioni, inoltre ogni evento è sconnesso dagli altri.
• $S$ è l’evento certo mentre l’insieme nullo è l’evento nullo. Per il lancio di due monete (costituite da testa e croce) lo spazio dei campioni è costituito da tutte le coppie che possono uscire ($2^2$), ovvero $\{TT,TC,CC,CT\}$, l’evento “si ottiene una testa e una croce” è composto dal sottoinsieme $\{TC,CT\}$ quindi 2/4 → ½ di probabilità. Da qui traiamo la definizione classica ed intuitiva della probabilità di verificarsi di un evento $A$ ovvero il rapporto tra i casi favorevoli $f_A$ ed il numero di casi totali $n$ la formalizzazione matematica sarebbe:

Formula generale per la probabilità

$P(A)=\frac{f_A}{n}$ con la notazione $P(A)$ si intende la probabilità che l’evento $A$ accada

• Prendendo in esame l’esperimento del lancio del dado e l’evento “Esce un numero inferiore a 3” lo spazio dei campioni è costituito da tutte i possibili esiti del lancio, ovvero $S=\{1,2,3,4,5,6\}$ e gli esiti favorevoli sono solo $2$ ovvero $\{1,2\}$. Quindi la probabilità di tale evento è $\frac{2}{6}$ .

Mutualmente esclusivi

Se due eventi A e B non hanno elementi in comune essi sono detti eventi disgiunti o mutualmente esclusivi perché l’occorrenza dell’uno esclude l’altro.

^81d10b

Definizione frequentista

La definizione classica non considerava la possibilità di eventi non equiprobabili (come un dato truccato ad esempio), fu Richard von Mises a definire la probabilità che accada un evento $A$ come il limite del rapporto tra il numero di volte in cui si è verificato l’esito $f_A$ (l’esito favorevole) e il numero degli esperimenti $n$ ovvero:

Formula frequentista per la probabilità

$P(A)={\lim }_{n\to \infty }\frac{f_A}{n}$

La definizione frequentista ha un problema di fondo insuperabile: non tutti gli esperimenti sono ripetibili e quindi alcune probabilità non sarebbero calcolabili. Da qui nasce la teoria della probabilità

---

Teoria della probabilità

Siano $A$ e $B$ due eventi qualsiasi definiti su uno spazio dei campioni $S$. Di seguito gli assiomi della probabilità:

Assiomi della probabilità

1. $0\le P(A)\le 1$
2. $P(S)=1$ e $P(\varnothing )=0$
3. $P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Il terzo assioma afferma che la probabilità che si verifichi o $A$ o $B$ è uguale alla probabilità di $A$ più la probabilità di $B$ meno la probabilità che si verifichino entrambe. Usando il formalismo logico questo assioma può essere riscritto così: $P(A\vee B)=P(A)+P(B)-P(A\wedge B)$

La distribuzione di probabilità è detta uniforme se tutti gli eventi sono equiprobabili

---

Probabilità condizionata e indipendenza

Il verificarsi di alcuni eventi può cambiare le probabilità che si verifichi un altro evento. La probabilità di un evento A, condizionata al verificarsi di un evento B (non nullo) è definita come:

Probabilità di A, dato B già verificato

$P(A|B)=\frac{P(A\cap B)}{P(B)}$

Definendo questa cosa capiamo che due eventi si dicono indipendenti se:

• $P(A|B)=P(A)$
• $P(B|A)=P(B)$ Da questa definizione possiamo ricavarci la formula per calcolare la probabilità che $A$ e $B$ accadano in questo modo:

Probabilità che sia l'evento $A$ che l'evento $B$ accadano

$P(A\wedge B)=P(A)\ast P(B)$

É importante anche ricordare il concetto di indipendenza degli eventi, ovvero molti eventi anche se sembrano correlati sono completamente indipendenti

Esempio di indipendenza

Domanda: Lanciamo un dado 3 volte. La probabilità della sequenza $[2,1,6]$ è più alta della probabilità della sequenza $[3,3,3]$? Risposta: No, le due probabilità sono uguali. Infatti $P([2,1,6])$ = $P([3,3,3])=\frac{1}{6}\ast \frac{1}{6}\ast \frac{1}{6}=\frac{1}{216}$

---

Regola di Bayes

Dalla definizione di probabilità condizionata, si ricava la regola di Bayes, importante in molti campi come quello dell’intelligenza artificiale. Come possiamo notare in questa immagine la probabilità di un evento A condizionata dal verificarsi di un evento B è uguale alla probabilità di un evento B condizionata da un evento A ovvero $P(A\wedge B)=P(B\wedge A)$, da qui nasce la regola di Bayes ovvero:

Regola di Bayes

$P(B|A)=\frac{P(A|B)\ast P(B)}{P(A)}$

Arriviamo a questa formula in questo modo:

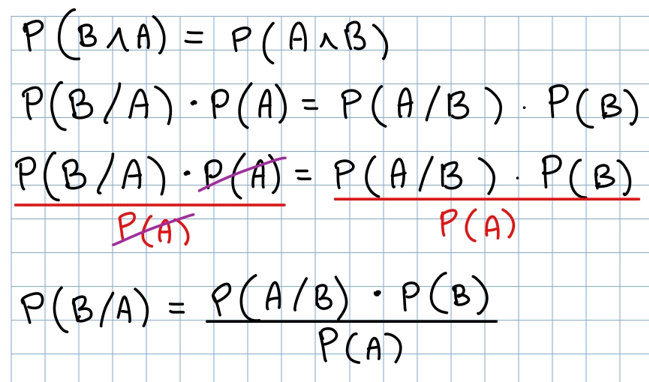
La regola di Bayes ci permette quindi di calcolare $P(B|A)$ usando solo:

• $P(A)$
• $P(B)$
• $P(A|B)$ Esempio:
• $P(E)=\frac{1}{10}$ ; $P(S)=\frac{4}{10}$ ; $P(S|E)=\frac{7}{10}$ Quindi $P(E|S)=\frac{P(S|E)\cdot P(E)}{P(S)}=\frac{\frac{7}{10}\cdot \frac{1}{10}}{\frac{4}{10}}=\frac{7}{40}$

---

Teorema della probabilità totale

Qualche volta il calcolo della probabilità di un evento deve mettere in conto più processi casuali.

Teorema: Sia A un evento e siano $B_1,B_2,...,B_n$ eventi mutuamente esclusivi tali che $P(B_i)\ne 0$ per ogni i ed inoltre $P(B_1||B_2||...||B_n)=1$

Formula della probabilità totale

$P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+\cdots +P(A|B_n)P(B_n)={\sum }_{i=1}^{n}P(A|B_i)P(B_i)$ ovvero la sommatoria di tutte le probabilità che A accada se $B_i$ accade

Dimostrazione Dal momento che gli eventi $B_1,B_2,...,B_n$ sono esaustivi ovvero almeno una di loro si deve verificare. Siccome sono anche mutualmente esclusivi la probabilità che $A$ si verifichi è la somma che sia $A$ che $B_i$ si verifichi ovvero:

• $P(A)=P(A\cap B_1)+\cdots +P(A\cap B_n)$ Dalla definizione di probabilità condizionata sappiamo che per ogni i:
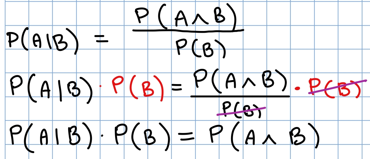• $P(A\wedge B_i)=P(A|B_i)\cdot P(B_i)$ La formula che usiamo la ricaviamo in questo modo. A questo punto il teorema è dimostrato

Esempio:

Supponiamo di divedere un mazzo di carte (52 carte) in due mazzi:

• $M_1$ con $30$ carte
• $M_2$ con $22$ carte Supponiamo che in $M_1$ ci siano 3 dei 4 assi. Mentre in $M_2$ c’è il quarto asso. Scegliendo un mazzo a caso quale è la probabilità di pescare un asso? (definiamo questa probabilità con $P(A)$:
• $P(M_1)=\frac{1}{2}$ probabilità di scegliere $M_1$ tra i due mazzi.
• $P(M_2)=\frac{1}{2}$ probabilità di scegliere $M_2$ tra i due mazzi.
• $P(A|M_1)=\frac{3}{30}=\frac{1}{10}$ probabilità di prendere un asso scegliendo il mazzo $M_1$
• $P(A|M_2)=\frac{1}{22}$ probabilità di prendere un asso scegliendo il mazzo $M_1$ per il teorema della probabilità totale: $P(A)=P(M_1)\ast P(M_2)\ast P(A|M_1)\ast P(A|M_2)=\frac{3}{30}\cdot \frac{1}{2}+\frac{1}{22}\cdot \frac{1}{2}=\frac{4}{55}$

---

Problemi d’urna

Tutti gli eventi che si possono formalizzare come “Estraiamo una o più palline numerate, da una o più urna” vengono detti Problemi d’urna. É importante che le estrazioni siano non truccate e che ogni estrazione sia indipendente dalla precedente. Le estrazioni da un’urna si possono classificare in 4 modi: Attraverso i problemi dell’urna possiamo rispondere alla seconda domanda iniziale: Risposta 2:

• La probabilità di sbagliare il primo tentativo è $\frac{10^5-1}{10^5}$
• La probabilità di sbagliare il secondo tentativo è $\frac{10^5-2}{10^5-1}$
• La probabilità di sbagliare il terzo tentativo è $\frac{10^5-3}{10^5-2}$ la probabilità totale diventa:

---

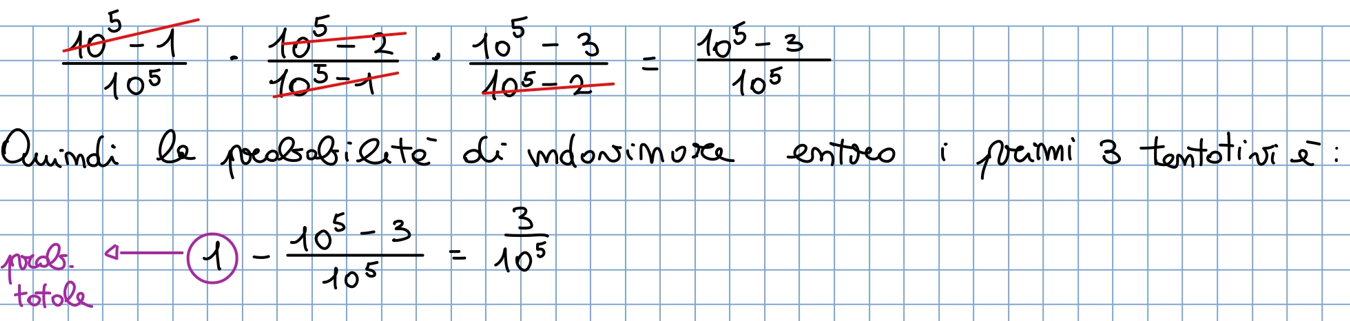
Paradosso del compleanno

Di seguito risponderemo alla domanda 4 posta all’inizio, ovvero “Se dovessi scommettere che in un’aula con 20 persone, ce ne siano almeno 2 che fanno il compleanno lo stesso giorno, scommetterei di si oppure no? E se ce ne sono 30, 40, 50 o più di persone?“. In pratica ci stiamo chiedendo se dato un certo numero di persone la probabilità che 2 di esse facciano il compleanno lo stesso giorno sia maggiore di $\frac{1}{2}$. Questo problema è noto con il nome di paradosso del compleanno non perché genera un paradosso ma perché la risposta è apparentemente controintuitiva.

TIP

Per il pigeonhole principle potremo dire che in un’aula con 366 persone di sicuro almeno 2 fanno il compleanno lo stesso giorno

Rispondiamo prima a “Qual è il numero minimo di persone presenti in un aula tale che la probabilità che due di esse siano nate lo stesso mese è maggiore di $\frac{1}{2}$”

TIP

Per il pigeonhole principle potremo dire che in un’aula con 13 persone di sicuro almeno 2 fanno il compleanno lo stesso mese

Assumiamo che $n$ sia uguale a $3$. Quindi abbiamo tre persone $p_1$,$p_2$ e $p_3$ ed ognuna di esse può essere nata in uno dei $12$ mesi. Il numero di terne ( {mese di nascita di $p_1$, mese di nascita di $p_2$, mese di nascita di $p_3$} ) possibili è dato dal numero di disposizioni semplici ovvero $12^3=1728$ (numero casi totali). Il numero di casi dove tutti e 3 i mesi sono diversi è:

• $3!\cdot \left(\genfrac{}{}{0ex}{}{12}{3}\right)=3!\cdot \frac{12!}{3!9!}=12\cdot 11\cdot 10=1320$ Moltiplichiamo tutto per $3!$ perché sono 6 le combinazioni che possiamo fare dati 3 mesi. La probabilità che tre persone siano nate in un mese diverso con $n=3$ è $\frac{1320}{1728}=0,76$

Ritornando alla domanda inziale, dobbiamo prendere in esame i casi in cui in aula ci siano meno di 366 persone. Calcoliamo la probabilità che facciano tutti il compleanno in giorno diverso e partiamo dal caso peggiore ovvero un anno bisestile:

• Se $n=2$ abbiamo $365$ su $366$ giorni possibili per la seconda, se devono essere giorni diversi. Quindi, la probabilità che siano nati in giorni diversi è $\frac{365}{366}=0,997$.
• Se $n=3$ abbiamo $365$ su $366$ giorni possibili per la seconda, e $364$ su $366$ per la terza, se devono essere giorni diversi. Quindi, la probabilità che siano nati in giorni diversi è $\frac{365\cdot 364}{366^2}=0,991$

Formula paradosso del compleanno

Se abbiamo $p$ persone la formula che usiamo per calcolare la probabilità che siano nate in giorni diversi è:

• $P_d(p)=\frac{p!\cdot \left(\genfrac{}{}{0ex}{}{366}{p}\right)}{366^p}$ Quindi la formula per calcolare la probabilità che almeno 2 persone facciano il compleanno lo stesso giorno è:
• $P(p)=1-P_d(p)=1-\frac{365\cdot 364\cdot \dots \cdot (366-p+1)}{366^{p-1}}$

Esempio

Per $p$ = 23 $P_d(23)=\frac{365\cdot 364\cdot \dots \cdot 344}{366^{22}}\approx 0.48$ $P(23)=1-0.48=0.52$

Risposta 4: Dall’esempio qua sopra capiamo che basterebbero 23 persone scelte a caso per avere più del 50% di probabilità che 2 persone facciano il compleanno lo stesso giorno.

---

Variabile casuale o valore atteso

Variabile Casuale Una variabile casuale è una funzione che associa ad ogni risultato possibile di un esperimento casuale un numero reale. In altre parole, ogni volta che si verifica un evento nel contesto di un esperimento (per esempio, lanciando un dado), la variabile casuale restituisce un valore numerico. Un esempio classico è il lancio di un dado. In questo caso, la variabile casuale X può rappresentare il numero che appare sulla faccia del dado. Quindi, quando lanci il dado, X prenderà uno dei seguenti valori: 1, 2, 3, 4, 5 o 6.

Valore Atteso Il valore atteso (o media ponderata) di una variabile casuale è il valore medio che ti aspetti di ottenere se ripeti l’esperimento un numero molto grande di volte. È un concetto che descrive la “tendenza centrale” della variabile casuale.

Per calcolare il valore atteso $E[X]$ di una variabile casuale X, moltiplichi ogni valore possibile che X può assumere per la probabilità che quel valore si verifichi e poi sommi tutti i risultati. La formula è la seguente:

Formula per il calcolo del valore atteso

$E[X]={\sum }_{x}x\cdot P[X=x]$

Dove:

• $x$ è un possibile valore che la variabile casuale $X$ può assumere.
• $P[X=x]$ è la probabilità che $\ast \ast X\ast \ast$ assuma il valore $x$.

Lancio di un Dado

Nel caso del lancio di un dado, la variabile casuale $X$ rappresenta il numero che appare sulla faccia del dado. I possibili valori di $X$ sono 1, 2, 3, 4, 5, e 6, e ognuno ha una probabilità di $\frac{1}{6}$ di verificarsi, perché il dado è equilibrato. Per calcolare il valore atteso $E[X]$: $E[X]=1\cdot P[X=1]+2\cdot P[X=2]+3\cdot P[X=3]+4\cdot P[X=4]+5\cdot P[X=5]+6\cdot P[X=6]$ Poiché la probabilità di ciascun numero è $\frac{1}{6}$, otteniamo:

• $E[X]=1\cdot \frac{1}{6}+2\cdot \frac{1}{6}+3\cdot \frac{1}{6}+4\cdot \frac{1}{6}+5\cdot \frac{1}{6}+6\cdot \frac{1}{6}$ Semplificando, otteniamo:
• $E[X]=\frac{1+2+3+4+5+6}{6}=\frac{21}{6}=3.5$ Quindi, il valore atteso del lancio di un dado è 3.5. Questo significa che, in media, se lanci un dado un numero molto grande di volte, il valore medio dei risultati sarà 3.5.

---

Linearità del Valore Atteso Una delle proprietà importanti del valore atteso è che è lineare, cioè:

• $E[X+Y]=E[X]+E[Y]$ Questo significa che se hai due variabili casuali X e Y, e le sommi, il valore atteso della somma sarà la somma dei valori attesi delle singole variabili. Per esempio, supponiamo di avere due variabili casuali: X, che rappresenta il lancio di un dado, e Y, che rappresenta un altro lancio di dado. Se calcoliamo il valore atteso della somma $X+Y$, avremo: $E[X+Y]=E[X]+E[Y]$ Poiché ciascun dado ha valore atteso 3.5, allora: $E[X+Y]=3.5+3.5=7$. Quindi, se sommiamo i risultati di due lanci di dado, ci aspettiamo che la media dei risultati sia 7.

Esempio

Domanda: Se lanciamo 2 dadi, qual è il valore atteso del massimo dei 2 valori.

In questo caso abbiamo quindi 36 casi possibili $\{(1,1),(1,2),...,(6,5),(6,6)\}$:

• Di coppie con “6” ne abbiamo 11
• Di coppie con “5” ma senza “6” ne abbiamo 9
• Di coppie con “4” ma senza “5” o “6” be abbiamo 7
• Di coppie con “3” ma senza “4”, “5”, o “6” ne abbiamo 5
• Di coppie con “2” ma senza “3”, “4”, “5” o “6” ne abbiamo 3
• Di coppie con solo “1” ne abbiamo solo 1.

Quindi:

---

Prova di Bernoulli

La prova di Bernoulli è un esperimento probabilistico che ha esattamente due risultati: successo(p) o fallimento(q = 1 - p). Il numero atteso dei numeri di tentativi da fare per ottenere “successo” è dato da 1/p. Esempi:

Dunque la legge dei grandi numeri detta anche teorema di Bernoulli ci garantisce che la media dei risultati ottenuti dopo un grande numero di tentativi si avvicina al valore atteso, quindi se lanciamo all’infinito un dado, la media ottenuta sarà esattamente $3,5$.

---

Giochi e paradossi probabilistici

Questo parte esplora quattro famosi paradossi probabilistici: il paradosso dei due bambini, il paradosso delle tre carte (o scatole), il paradosso dei tre prigionieri e il paradosso di Monty Hall.

1. Paradosso dei Due Bambini

• Problema: Un professore di probabilità ha due figli. Uno di loro è un maschio. Qual è la probabilità che anche l’altro figlio sia maschio?
• Soluzione: Ci sono quattro possibili combinazioni di genere per due figli: FF, FM, MF, MM. Sapendo che almeno uno è maschio, escludiamo FF. Rimangono tre possibilità: FM, MF, MM. Solo una di queste (MM) vede entrambi maschi. Quindi la probabilità è 1/3.

---

2. Paradosso delle Tre Carte (o Scatole)

• Problema (Versione Carte): Ci sono tre carte: una rossa su entrambi i lati (R), una bianca su entrambi i lati (B) e una rossa da un lato e bianca dall’altro (M). Si sceglie una carta a caso e si mostra un lato. Se il lato visibile è rosso, qual è la probabilità che anche l’altro lato sia rosso?
• Problema (Versione Scatole): Ci sono tre scatole: una con due monete d’oro (G2), una con due monete d’argento (A2) e una con una moneta d’oro e una d’argento (AG). Si sceglie una scatola a caso e si estrae una moneta. Se la moneta estratta è d’oro, qual è la probabilità che anche l’altra moneta nella scatola sia d’oro?
• Soluzione: Concentrandoci sulla versione delle carte, ci sono sei possibili scenari considerando entrambi i lati di ogni carta (Ra, Rb, Ma, Mb, Ba, Bb). Se il lato visibile è rosso, le possibilità sono Ra, Rb, Ma. Di queste, due (Ra, Rb) hanno anche l’altro lato rosso. Quindi la probabilità è 2/3.

---

3. Paradosso dei Tre Prigionieri

• Problema: Tre prigionieri (A, B, C) sono condannati a morte. Il re ne grazierà uno a caso. Il carceriere sa chi sarà graziato. A chiede al carceriere di dirgli quale tra B e C sarà giustiziato. Il carceriere dice che sarà giustiziato B. A pensa che ora la sua probabilità di essere graziato sia aumentata da 1/3 a 1/2.
• Soluzione: Prima della risposta del carceriere, la probabilità di A di essere graziato è 1/3. Ci sono due scenari in cui il carceriere dice che B sarà giustiziato:
  • C è graziato (probabilità 1/3).
  • A è graziato e il carceriere sceglie B a caso (probabilità 1/3 * 1/2 = 1/6). La probabilità totale che il carceriere dica che B sarà giustiziato è 1/3 + 1/6 = 1/2. Dato che il carceriere ha detto che B sarà giustiziato, la probabilità che C sia graziato è (1/3) / (1/2) = 2/3, mentre la probabilità che A sia graziato è (1/6) / (1/2) = 1/3. Quindi A si sbaglia.

---

4. Paradosso di Monty Hall

• Problema: Ci sono tre porte. Dietro una c’è un’auto, dietro le altre due ci sono delle capre. Il concorrente sceglie una porta. Il conduttore (che sa dove si trova l’auto) apre una delle altre due porte, rivelando una capra. Il conduttore offre al concorrente la possibilità di cambiare la sua scelta con la porta rimanente. Conviene cambiare?
• Soluzione: Sì, conviene cambiare. Inizialmente, la probabilità di scegliere la porta con l’auto è 1/3. Quindi, la probabilità che l’auto sia dietro una delle altre due porte è 2/3. Quando il conduttore apre una porta con una capra, quella probabilità (2/3) si concentra sulla porta rimanente.

---

Domanda Finale

• Problema: Ci sono 10 buste, una contiene un milione di euro, le altre sono vuote. Si sceglie la busta numero 1. Conviene scambiarla con le altre 9? E se qualcuno apre 8 delle altre 9 buste, rivelando che sono vuote, conviene scambiare la busta 1 con l’unica rimasta?
• Risposta: Inizialmente, la probabilità di avere il milione è 1/10. Scambiare con le altre 9 aumenta la probabilità a 9/10. Dopo che 8 buste vuote sono state aperte, la probabilità che il milione sia nella busta rimanente è diventata 9/10, mentre la probabilità che sia nella busta 1 è ancora 1/10. Quindi, conviene decisamente scambiare.

Questo riassunto fornisce una panoramica dei concetti chiave discussi nel documento, evidenziando i problemi, le soluzioni e le logiche alla base di ciascun paradosso.